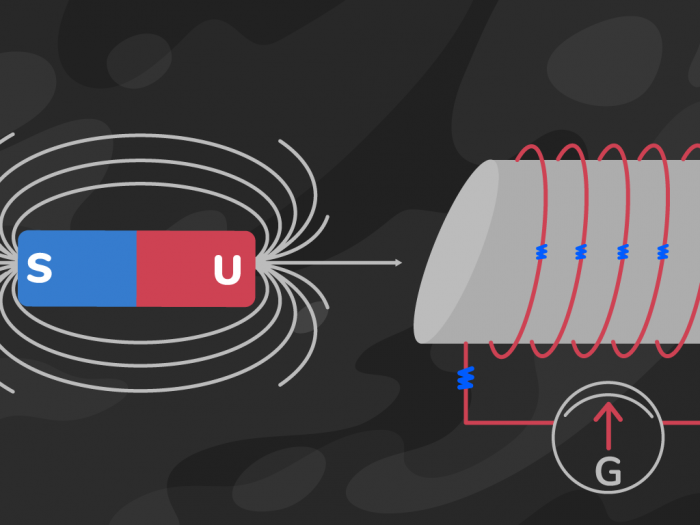
Induksi Elektromagnetik adalah salah satu kemajuan ilmiah paling penting yang mempengaruhi kehidupan manusia. Induksi elektromagnetik ditemukan oleh Michael Faraday pada tahun 1831. Secara resmi, ia…
Honda HR-V menjadi salah satu SUV terlaris di Indonesia, bahkan mengalahkan pesaingnya seperti Hyundai Creta, Toyota Yaris Cross, dan Chery Omoda 5. Apa yang membuat…
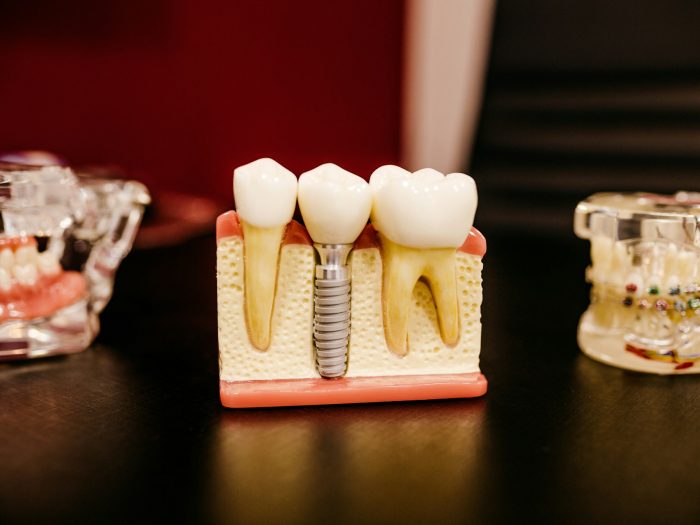
Implan gigi adalah solusi terbaik untuk memperbaiki penampilan, selain itu juga memberikan fungsi dan rasa yang sama seperti gigi asli. Implan gigi dapat dipakai dalam…
Pengelolaan limbah menjadi sangat krusial ditengah isu lingkungan yang semakin mengkhawatirkan. Inilah saatnya bagi semua pihak bekerjasama menerapkan prinsip kelestarian lingkungan hidup yang berkelanjutan. Ini…
Games dengan tema makanan dan kuliner bisa jadi pilihan terbaik untuk mengatasi rasa penasaran si Kecil. Saya sebagai orang tua, merasakan sendiri bahwa usia balita…